 |
Modeling protein structure and dynamics is nowadays critical for the understanding of the functioning of living cells as well as of their malfunction leading, e.g., to cancer or hereditary diseases. This research is thus significant in drug design. Currently, there are about 87,000,000 known protein sequences stored in the UniProt database (www.uniprot.org) (about 500,000 of which were verified and manually annotated), while the number of solved structures in the PDB database (www.rcsb.org) [17] is only 121,460. Therefore, modeling (prediction) of protein structure has nowadays become a standard procedure in biochemistry, biophysics, and biomedicine. Knowledge-based (bioinformatics) methods appear to be the most efficient ones at the moment [24]; however, they are database-dependent and, moreover, make increasing use of force fields. Simulations with empirical force fields become even more critical when studying protein folding pathways and free-energy landscapes, where the experimental data (from, e.g., fluorescence measurements or atomic-force microscopy) provide only fragmentary information of the structural changes or of the conformational space.
Despite the enormous progress in the development of all-atom force fields and efficient simulations techniques, as well as the construction of dedicated machines [12], all-atom molecular dynamics simulations are still restricted to small systems or short time scales. Moreover, extracting the important interactions and functionally important motions from the results of all-atom simulations is not easy and requires some aid from e.g., principal component analysis. Therefore the coarse-grained models, in which several atoms comprising a well-defined object are treated as one unit, become often the only ones with which to carry out large time- and size-scale simulations [7]. To date, most of the coarse-graining approaches are based on statistical potentials (such as, e.g., the CABS protein model developed in the Koliński group [8]); however, these approaches are limited by the completeness of structural databases and abundance of data that can be retrieved from the databases.
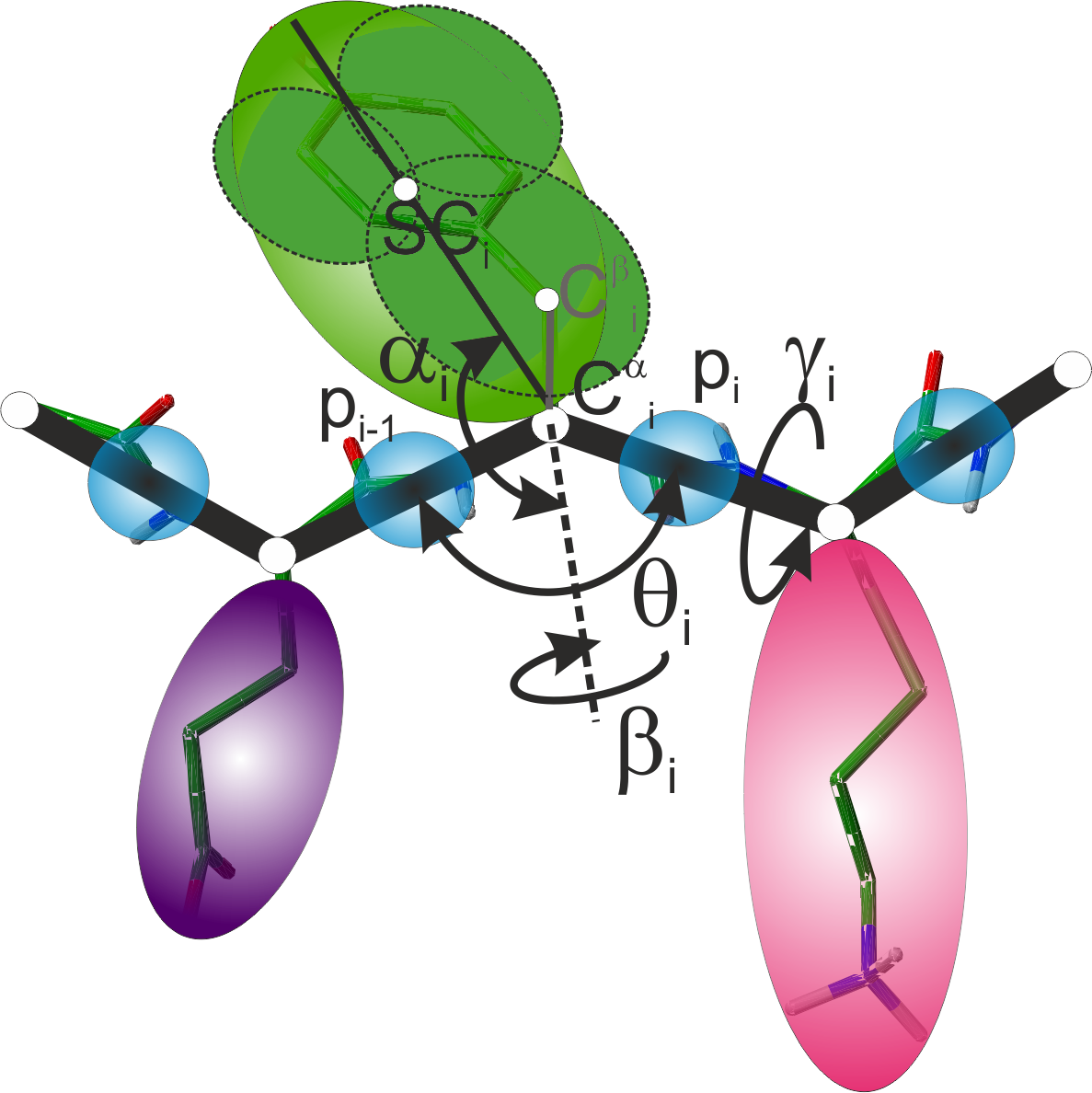
Our research group is since long developing the coarse-grained UNRES model of proteins (Figure 1) [15,14,13,26], which enables us to perform simulations by several orders of magnitude faster compared to that of all-atom simulations. At the same time, the corresponding force field has a close connection to the physics of interactions because it is based on the potential of mean force of the system under study in water, which is further expanded into Kubo's cluster cumulants [11], which correspond to the contributions to the effective energy function [15,23]. This feature clearly distinguishes the UNRES force field from other coarse-grained force fields, which are based on statistical potentials [7], are constructed in a neo-classical manner by analogy to all-atom potentials [18] or, as the Gō-like models [4], are designed for a particular protein to make its native structure the global minimum in the potential-energy surface. Use of the cluster-cumulant expansion results, naturally, in multibody terms, which are necessary to handle regular secondary structure properly with the coarse-grained force fields [9,15] and which are obtained in other force field in a heuristic manner [7]. Without using database information, the UNRES model has a relatively high prediction capacity, which was confirmed in the recent Community Wide Experiments on the Critical Assessment of Techniques for Protein Structure Prediction (CASP; predictioncenter.org) [3,10]. This model was also used with success to study protein-folding kinetics [27], protein free-energy landscapes [16] and biological processes [2,19]. Nevertheless, the UNRES model provides only a 5-6 Å resolution for about 60-residue proteins on average and does not always reproduce correct secondary structure.
 |
Recently we developed a rigorous approach to the derivation of the analytical expressions for he contributions to the effective energy functions in coarse-grained systems, which is based on expressing the energy by interatomic distances and expressing the distances as functions of the angles for collective rotations the atoms comprising the interaction sites about the virtual-bond axes. The torsional and correlation potentials derived with the use of this formalism are substantially different from those implemented in the present UNRES because they include the dependence on the virtual-bond-angles θ (Fig. 1). The form of this dependence agrees with the statistics derived from the PDB database and explains why the θ angles are large for extended structures and close to 90° for α-helical structures [23]. This observation indicates that a correct representation of local interactions has a critical influence both on local geometry and on the correct description of secondary structure. Therefore, the derivation of correct functional forms of the torsional and correlation potentials should result in a major improvement of both the accuracy of local structure and the reproduction of secondary structure and, consequently, increase the capability of UNRES to predict tertiary structure significantly. Moreover, our recent research demonstrated that the torsional and correlation potentials should be split into backbone and backbone-and-side-chain contributions; the potentials used in the current UNRES encompass the backbone and Cβ atoms, while the side-chain contributions are only partially represented by additional torsional potentials [22]. Replacement of the current functional forms for the torsional and correlation potentials should, therefore, result in major improvement of the accuracy of local structure and to the correct reproduction of secondary structure; consequently, it should significantly enhance the capability of UNRES to model protein structure and dynamics, including database-free prediction of protein structure. Furthermore, the formalism introduced in our recent work [23] enables us to derive physics-based formulas for the local side-chain-interaction potentials (that depend on the side-chain α and β angles of Figure 1) that take into account chirality change, which is important in the simulations of system in which this process takes place (e.g., in αA-crystallin [5], where it is the cause of the senile cataract).
Protein simulations with UNRES are carried out by means of Langevin dynamics. Because the variables are the Cα···Cα and Cα···SC virtual-bond vectors, the full inertia matrix appears in the equations of motion [6], this restricting the size of a system to about 1300 amino-acid residues because the memory required scales with the square of system size. The change of coordinates to Cartesian coordinates of the Cα and Cβ atoms will reduce the inertia matrix to the symmetric pentadiagonal (quindidiagonal) form, the inversion [1] and diagonalization [20] of which requires memory that scales linearly with system size. We have already implemented the cut-off on long-range interactions in UNRES [21]; therefore, with the change of coordinate representation, simulations of large systems will be possible to run.
Go to main page